Bevezetés a numerikus módszerekbe
12.1. Megoldás VEM segítségével
- Nyissuk meg az Ansys Workbench programot, majd hozzunk létre egy tranziens hőtani blokkot, melyben a vizsgálatainkat fogjuk végezni! A 12.1. ábrán látható módon a SpaceClaim program segítségével a legkényelmesebb létrehozni a 10 cm átmérőjű gömböt mint testprimitívet, melyet vizsgálunk. A probléma esetünkben bár 3 dimenziós, valójában a gömbszimmetria miatt egy dimenzióra redukálható. Ha ezt nem is tesszük meg, a gömb nyolcada is elég lenne a számításhoz. Bonyolultabb szimulációk esetén az ilyen egyszerűsítéseket erősen ajánlott megtenni, most a gyorsabb eredményre jutás miatt ezt a precizitást elengedjük. Ez a szemlélet a legegyszerűbb út megkeresése, ugyanis a munkáltatónak is pénzbe kerül a mérnök ideje, ezért a valóságtól távol áll egy egyszerű probléma végletekig való egyszerűsítése, ha az bár matematikailag bonyolultabb módszerekkel, de lényegesen gyorsabban megoldható.
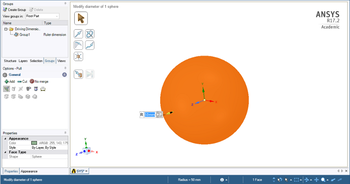
- A kihúzás (Pull) parancs segítségével a gömbfelületre kattintva hagyjuk meg az 50 mm-es sugarat, majd a mellette megjelenő kék P-re kattintsunk, így tudjuk publikálni paraméterként az alma átmérőjét! Konstatáljuk, hogy a modellfa alatt a csoportok (Groups) fülön megjelent a paraméter, ahogy az a 12.2. ábrán látszik, illetve a geometria alatt a munkalapon is. A paraméterek lesznek segítségünkre akkor, ha számos geometriai variánst, peremfeltételt, kezdeti feltételt, vagy épp anyagjellemzőt szeretnénk megvizsgálni, az eredmény pedig jól jellemezhető egy vagy néhány számértékkel. Ezzel az eszköztárral vagy a beépített vagy külső algoritmusok segítségével optimalizációt végezhetünk. Az optimumkeresést egy későbbi feladatban mutatjuk be.
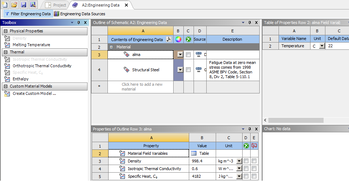
- Az anyagjellemzők (Engineering Data) alblokkban definiáljunk az alma anyagjellemzőit a 12.1. táblázat alapján, ahogy az a 12.3. ábrán látható! Az alapértelmezett szerkezeti acél anyagjellemzőit minden további nélkül módosíthatjuk, a belső adatbázis számadatait így nem tudjuk átírni. Azaz ha új szimulációt indítunk, a szerkezeti acél anyagjellemzői visszaállnak eredeti értékükre. De új anyagot is létrehozhatunk a megjelölt anyagi tulajdonságokkal. Itt megjegyezzük, hogy az alma anyagát izotrópnak feltételezzük, azonban az anyagjellemzők eszköztárban látható, hogy az egyes jellemzők irányfüggő változatai is megadhatók, melyek például kompozit szerkezetek esetén fontosak. Bár egy anyagnak jóval több fizikai tulajdonsága létezik, mint amit láthatunk itt, a szimuláció bonyolításával, más fizikai modellek szimulációba való beillesztésével automatikusan bővül a kínálat az adatbázisban szereplő anyagok esetén. Így sosem kell attól tartanunk, hogy elég anyagjellemzőt adtunk-e meg a modell lefutásához. Azonban ha direkt vagy véletlenül hozzáadunk anyagjellemzőket egy anyaghoz, a projekt fülön az anyagjellemzők mellett a zöld pipa megváltozik. Amíg nem töröltük ki a felesleges adatot vagy nem töltöttük ki a megfelelő mezőket, számos hibaüzenettel fogunk találkozni a későbbi lépések folyamán. A jelenlegi példában egy új anyagot hoztunk létre a személetesség kedvéért a szerkezeti acél mellett, ami több anyagból álló szerkezet esetén szükséges lehet. A hozzáadott anyagjellemzők: izortóp hővezetési tényező, sűrűség és fajhő.
- Indítsuk el a modellezőt, állítsuk be a geometria fülön belül az alma anyagát, ahogy ezt a 12.4. ábra mutatja, majd adjuk meg kezdeti feltételnek a 30 °C-os hőmérséklet értéket!
- Állítsuk be a szimulációs beállításokban (Analysis Settings) a végső időlépés (Step End Time) értékét 25000 s-ra, míg az időlépés legyen 48 s, tehát manuálisan definiáljuk az időbeli diszkretizációt!
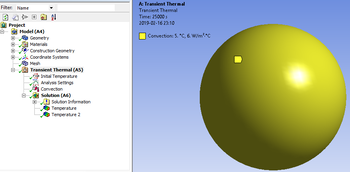
- Generáljuk le az alaphálót, majd állítsuk be a szükséges peremfeltételeket a következő módon Kattintsunk a tranziens hőtani (Transient Thermal (A5)) részre, jelöljük ki a gömb felületét, majd jobb klikk után a beszúrás menüből válasszuk a hőátadást (Convection) Adjuk meg az áramló levegő hőmérsékletét és a hőátadási tényezőt [5 °C és 6 W/(m2·K)], ahogy ez a 12.5. ábrán látható! A kezdeti hőmérsékletet, a környező levegő hőátadási tényezőjét, illetve a környező levegő hőmérsékletét adjuk meg paraméterként a későbbi vizsgálatok érdekében. A megoldás részben pedig kérjünk le egy hőmérséklet és egy hőáram mezőt a teljes geometriára vonatkozóan: beszúrás → termikus → hőmérséklet és teljes hőáram (Total Heat Flux) Ez a hőáram abszolút értékét jeleníti meg, azonban lehetőség van a jellemző irány menti lekérdezésére is, mivel vektoriális mennyiségről van szó. Adjunk hozzá a modell fülhöz jobb klikk után a szerkesztési geometria (Construction Geometry) alblokkot, amelyen belül definiáljunk egy útvonalat (Path) a gömb belső pontja (0/0/0) és fala (0/0/0,05 m) között. Ha a megadott egyenes túlnyúlik a számítási téren, a program automatikusan csak a vizsgált térben közli az eredményeket. Ehhez is kérjünk le egy hőmérsékletmezőt a megoldás részben az előzőek alapján, azonban itt az elemzési eljárást (Scoping Method) állítsuk át útvonalra, majd jelöljük ki a vizsgálni kívánt útvonalat! Így lehetőségünk nyílik a minimum, maximum és átlaghőmérsékletek időbeli lekérdezése mellett az eredmények (itt hőmérséklet) egyenes menti lekérdezésére is. Az eredményt tartalmazó adatsort már könnyen tudunk exportálni például Excel táblázatba. Az útvonal segítségével kapott eredmények alapján végezzük el háló- és időfüggetlenségi vizsgálatot!
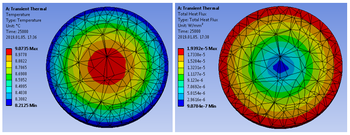
- Futtassuk le a szimulációt a megoldás paranccsal! Kattintsunk a hőmérsékletre, majd a teljes hőáramra az eredmények értékeléséhez, melyek a 12.6. ábrá láthatóak!Mivel hőt az alma a felszínén adja le, ezért várható volt, hogy a közepe marad a legmelegebb a szimuláció végén a perem- és kezdeti feltételek miatt. A peremen való hőelvonás eredményeképp a hőáramsűrűség pedig a peremeken lesz maximális és az alma közepén minimális.
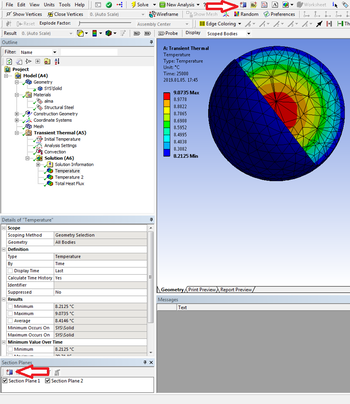
- A 12.6. ábrán látható metszetet a gömbből az új osztósík (New Section Plane) paranccsal képezhetjük. Egyszerre több sík mentén is elmetszhetjük az alakzatot és minden metszet esetében megadhatjuk, hogy a sík mely oldalára eső részt távolítsuk el. Ha szeretnénk, a metsző síkokat egyesével ki/bekapcsolhatjuk, illetve az eltávolított részt is módosíthatjuk utólag, ahogy ez a 12.7. ábrán látható.
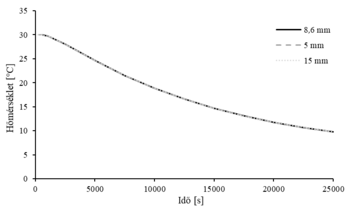
- Eddig az alapértelmezett hálóméretet alkalmaztuk, most nézzük meg, hogy a 8,6 mm-es elemméret mellett a 15 mm-es és az 5 mm-es elemméretek esetén hogyan változik a maximális hőmérséklet lefutása az időben! Az eredmény a 12.8. ábrán látható. Az egyes görbék kevesebb, mint 0,1 °C-kal térnek el egymástól, így kijelenthető, hogy az elemméretnek a vizsgált tartományban minimális hatása van az eredményre, így mindegyik hálóméret kiválóan alkalmazható a feladathoz. Az erőforrásokkal való spórolás miatt a 15 mm-es élhosszú háló a legjobb választás. Az időfüggetlenségi vizsgálatot később végezzük el, amikor a véges differencia módszer (VDM) segítségével is megkaptuk az eredményt.
- További feladat: végezzünk érzékenységvizsgálatot az alábbi paraméterek megadásának segítségével a következő jellemzőkre Az alma átmérője: 10 cm, 7,5 cm és 5 cm, a hőátadási tényező értéke 6, 60, és 600 W/(m2·K), az alma kezdeti hőmérséklete 30 °C, 40 °C és 50 °C, illetve a külső áramló levegő hőmérséklete 5 °C, 7,5 °C és 10 °C.
Tartalomjegyzék
- Bevezetés a numerikus módszerekbe
- Impresszum
- Elméleti rész
- Előszó
- 1. Bevezetés
- 2. Lineáris egyenletrendszerek
- 3. Nemlineáris egyenletek megoldása
- 4. Numerikus deriválás
- 5. Numerikus integrálás
- 6. Közönséges differenciálegyenletek
- 7. Stabilitás
- 8. Végeselemes alkalmazások
- A1 Függelék • A Lorenz-attraktor megoldásához használt MATLAB-kód
- A2 Függelék • Tisztán implicit diszkretizálású Fourier-egyenlet megoldásához használt MATLAB-kód
- A3 Függelék • A Fourier-egyenlet Θ-módszerrel való megoldásához tartozó MATLAB-kód
- A4 Függelék • A tranziens Fourier-egyenlet végeselemes megoldásához használt MATLAB-kód
- Irodalomjegyzék
- Előszó
- Példatár
- 9. A példák megoldására választott szoftverkörnyezet
- 10. A numerikus szimuláció lépései
- 11. Tranziens hővezetés 1D-ben és eredményértékelési lehetőségek egy elemi kocka példáján keresztül • Tranziens hőtani probléma
- 12. VEM, VDM, valamint közelítő analitikus megoldások összehasonlítása gömbi koordináta-rendszerben
- 13. Szigetelt gőzvezeték • Stacionárius hővezetés egy dimenzióban, optimalizálás
- 14. Bimetál • Kapcsolt stacionárius hővezetési-szilárdsági probléma
- 15. Kazánfal • Stacionárius hővezetési probléma kontakt hőellenállással, belső hőfejlődéssel és hősugárzással
- 16. Hűtött gázturbina lapát • Stacionárius hősugárzási-hőátadási probléma
- 17. Belső égésű motor dugattyúja • Tranziens hőátadási probléma
- 18. Processzor hűtőborda szimulációja hőcsővel és nélküle • Stacionárius hőátadási probléma
- Irodalomjegyzék a példatárhoz
- 9. A példák megoldására választott szoftverkörnyezet
Kiadó: Akadémiai Kiadó
Online megjelenés éve: 2019
ISBN: 978 963 454 335 0
Ez a jegyzet elsősorban a Kalorikus Gépek Numerikus Szimulációja tantárgy előadásaihoz tartozó segédanyagként készült szakdolgozat előtt álló BSc mérnökhallgatók számára.
Hivatkozás: https://mersz.hu/kovacs-jozsa-bevezetes-a-numerikus-modszerekbe//
BibTeXEndNoteMendeleyZotero